5. Типы в SystemVerilog

В SystemVerilog все данные представлены при помощи битвекторов, следует об этом помнить, ведь при работе на таком уровне абстракции бывает удобно взять какой-то конкретный бит — здесь это делать можно. Самих типов не так много, и часть из тех, что есть не может быть напрямую использованы в синтезируемой части кода. В таблице приведены все типы данных в SystemVerilog.

systemverilog datatypes
Рисунок 1. Типы в SystemVerilog[1]

Из них не синтезируются без лишних телодвижений real, realtime, time, shortreal, которые ведут себя привычным для программистов образом, так что в колонках, связанных с особенностями поведения в аппаратуре стоят пропуски.

Можно заметить важную колонку "2 state/4 state", значения в которой отличаются для logic и bit. Значения сигнала может принимать в общем 4 состояния, что показано на схеме.

values
Рисунок 2. Наглядное представление значений[2]

  1. С 0 и 1 всё понятно: это отсутствие и наличие сигнала.

  2. x означает, что сигнал неизвестен, например, при каком-то конфликте.

  3. z означает высокоимпедансное состояние, то есть выход ведёт себя как разомкнутая цепь: внешние устройства, подключенные к этому выводу, могут изменять напряжение на нём по своему усмотрению (в некоторых рамках), не влияя на работу схемы; и наоборот — схема не мешает внешним устройствам менять напряжение на контакте. Используется при отключении от шины, например, в многоточечных интерфейсах передачи данных для изоляции сигналов и предотвращения короткого замыкания.

Работа с float-ми

"Из коробки" в SystemVerilog нет поддержки чисел с плавающей запятой в синтезируемой части кода (зато есть в тестбенчах). Так что для работы с ними нужно либо брать готовые модули (в открытом доступе, например, Berkeley HardFloat или IP производителя), либо писать самому.

По стандарту IEEE 754[3] 32-битные числа с плавающей запятой представлены следующим образом.

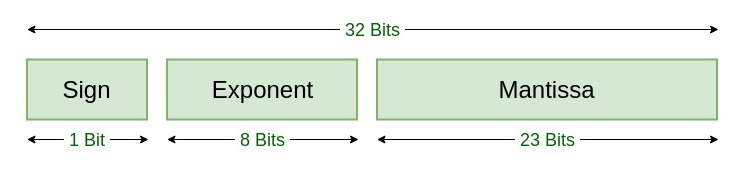
float 32
Рисунок 3. 32-битное представление чисел с плавающей запятой по стандарту IEEE 754[4]

Со следующей формулой декодирования.

Умножение byte на float

При реализации свёртки удобно считать, что ядро свёртки — это матрица и float-ов. Однако обрабатываемая картинка в формате grayscale — это матрица из byte-ов, таким образом необходимо продумать, как умножить byte на float. Исходя из формулы для декодирования 32-битных чисел с плавающей запятой, можно лего выразить следующее.

Получившийся результат может быть отрицательным и "вылезать" даже за границы float, необходимо привести результат к byte, мы примем такие соглашения.

  1. Если число больше 255, то считаем его равным 255.

  2. Если число меньше нуля, то мы считаем его равным 0.

Учитывая всё вышесказанное, реализуем модуль для умножения float на byte.

src/xx-types/float_mult_byte.sv
module float_mult_byte (
    input  logic [31:0] float_in,
    input  byte unsigned uint8_in,
    output byte unsigned uint8_out
);

  logic         sign;
  byte unsigned exponent; (1)
  logic [22:0]  mantissa;

  byte         exp_shift;
  logic [31:0] scaled_mantissa;
  logic [31:0] mantissa_to_uint;
  logic [31:0] uint_extended;
  logic [32:0] fraction_sum;

  always_comb begin

      sign          = float_in[31];
      exponent      = float_in[30:23];
      mantissa      = float_in[22:0];

      exp_shift = exponent - 8'd127;

      if ((exp_shift - 23) >= 0) (2)
        scaled_mantissa =
          ((mantissa * uint8_in) << (exp_shift - 23)) +
          (uint8_in << exp_shift); (3)
      else if (exp_shift >= 0) begin
        mantissa_to_uint = mantissa * uint8_in;
        uint_extended = uint8_in;
          scaled_mantissa =
            (mantissa_to_uint >> (-(exp_shift - 23))) +
            (uint_extended << exp_shift);
      end else begin
        mantissa_to_uint = mantissa * uint8_in;
        uint_extended = uint8_in;
        if ((uint_extended << (32 + exp_shift)) == 0)
          fraction_sum  = (mantissa_to_uint << (32 + (exp_shift - 23))); (4)
        else
          fraction_sum =
            (mantissa_to_uint << (32 + (exp_shift - 23))) +
            (uint_extended << (32 + exp_shift));
        scaled_mantissa =
          (mantissa_to_uint >> -(exp_shift - 23)) +
          (uint_extended >> -exp_shift) + fraction_sum[32]; (5)
      end

      if (scaled_mantissa > 255) begin (6)
        uint8_out = 8'd255;
      end else if (scaled_mantissa == 0 || sign) begin
        uint8_out = 8'd0;
      end else begin
        uint8_out = scaled_mantissa[7:0];
      end
    end

endmodule
1 byte в SystemVerilog — это знаковое 8-ми битное целое число, если нужно беззнаковое, то надо указать отдельно.
2 Так как мы умножаем на степень двойки, то эффективнее делать просто сдвиги. Для этого нужно понимать, куда сдвигать.
3 Если умножить результат сложения, то из-за сдвигов "потеряется" часть информации, и ответ будет неверный.
4 Единственная ситуация, когда из суммы дробных частей может появится дополнительная единичка: оба слагаемых умножаются на отрицательную степень двойки, тогда возникает две дробные части. Их надо учесть, fraction_sum — это сумма дробных частей чисел. Заметим, что оно 33-битное: в старшем бите лежит результат переполнения после выполнения сложения.
5 Учитываем целую часть суммы дробных частей.
6 Результат нужно привести к байту.
Обязательно порешайте упражнения.